Poker Test (Numerical Solution )

1. Define and develop a Poker test for four-digit random numbers. A sequence of 10,000 random numbers, each of four digits has been generated. The analysis of the numbers reveals that in 5120 numbers all four digits are different, 4230 contain exactly one pair of like digits, 560 contain two pairs, 75 have three digits of a kind and 15 contain all like digits. Use Poker test to determine whether these numbers are independent. (Critical value of chi-square test for α=0.05 and N=4 is 9.49).

 

 

Solution

 

The Poker Test is the test for independence based on the frequency with which certain digits are repeated with in a series of numbers. This test not only tests for the randomness of the sequence of numbers, but also the digits comprising of each of the numbers. The expected value of each of the combination of digits in a number is compared with the observed value by means of the chi-square test for independence. The acceptance is done if the observed value of chi-square sums for all the possible combinations of digits is less than the acceptable value for the given degree of freedom at the specified confidence interval.

 

Poker test for four digit numbers

 

In four digit number, there are five different possibilities

 

All individual digits can be different

There can be one pair of like digit

There can be two pair of like digits

There can be three digits of a kind

There can be four digits of a kind

The probabilities associated with each of the possibilities is given by

 

P (four different digits) = 4C4 * (10/10) * (9/10) * (8/10) * (7/10) = 0.504

 

P (one pair) = 4C2 * (10/10) * (1/10) * (9/10) * (8/10) = 0.432

 

P (two pair) = (4C2/2)*(10/10) * (1/10) * (9/10) * (1/10) = 0.027

 

P (three digits of a kind) = 4C3 * (10/10) * (1/10) * (1/10) * (9/10) = 0.036

 

P (four digits of a kind) = 4C4 * (10/10) * (1/10) * (1/10) * (1/10) = 0.001

 

Now the calculation table for the Chi-square statistics is:

Combination(i)	Observed Frequency(Oi)	Expected Frequency(Ei)	(Oi-Ei)	(Oi-Ei)2/Ei
Four different digits	5120	0.504*10000 = 5040	80	1.269
One pair	4230	0.432*10000 = 4320	-90	1.875
Two pair	560	0.027*10000 = 270	290	311.481
Three digits of a kind	75	0.036*10000 = 360	285	225.625
Four digits of a kind	15	0.001*10000 = 10	5	2.5
	10000	10000		Σ(Oi-Ei)2/Ei = 542.75

 

 

 

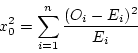    =   542.75

 

and Given X²_{a,N   =}   X²_0.05,4  = 9.49

 

Here the calculated value of chi-square is 542.75 which is greater than the given tabulated value of chi- square so we reject the null hypothesis of independence between given numbers.